TRIANGLE RULE

Triangle Law of Vector Addition

Statement of Triangle Law

If 2 vectors acting simultaneously on a body are represented both in magnitude and direction by 2 sides of a triangle taken in an order then the resultant(both magnitude and direction) of these vectors is given by 3rd side of that triangle taken in opposite order.

Derivation of the law

Consider two vectors P and Q acting on a body and represented both in magnitude and direction by sides OA and AB respectively of a triangle OAB. Let θ be the angle between P and Q. Let R be the resultant of vectors P and Q. Then, according to triangle law of vector addition, side OB represents the resultant of P and Q.

               

So, we have

                  R = P + Q

Now, expand A to C and draw BC perpendicular to  OC.

From triangle OCB,

             

In triangle ACB,

              

Also,

              

Magnitude of resultant:

Substituting value of AC and BC in (i), we get

              

which is the magnitude of resultant.

Direction of resultant: Let ø be the angle made by resultant R with P. Then,

From triangle OBC,

              

which is the direction of resultant.

How to Calculate Triangle Law of Forces - Definition, Formula and Example

Definition:

Triangle law of forces states that, If two forces acting at a point are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then the closing side of the triangle taken in the reversed order represents the resultant of the forces in magnitude and direction.

Formula:

a / sin A = b / sin B = c / sin C Where a, b, c = sides of a triangle A, B, C = angles between the sides of a triangle

Example 1 :

Find angle A, C and side c from side a = 5, side b = 6, angle B = 30 using triangle law of forces.^o

Solution:

Let us calculate the value of angle A from angle B.

Step 1:

In the given formula, take sin A on left hand side and multiply a with sin B divided by b which gives, sin A = (a x sin B) / b sin A = (5 x sin 30) / 6 A = sin^-1(0.4167) A = 24.624^o

Step 2:

Angle, A + B + C = π Therefore, C = π - A - B C = 180 - 24.624 - 30 C = 125.376^o

Step 3:

To calculate the value of c: In the given formula, take c on left hand side and multiply a with sin C divided by sin A which gives, c = (a x sin C) / sin A c = (5 x sin 30) / sin 24.624 c = 9.784

Example 2 :

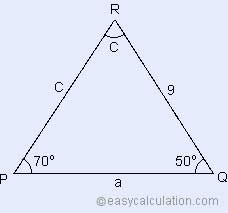
Find angle C, side a, c from side b = 9, angle A = 70^o, angle B = 50^o using triangle law of forces.

Solution:

Let us calculate the value of angle C, side a, side c from angle B.

Step 1:

To calculate the value of angle C: Angle, A + B + C = π C = π - A - B C = 180 - 70 - 50 C = 60^o

Step 2:

To calculate the value of a: In the given formula, take a on the left hand side and multiply b with sin A divided by the sin B which gives, a = (b x sin A) / sin B a = (9 x sin 70) / sin 50 a = 11.04

Step 3:

To calculate the value of c: In the given formula, take c on left hand side and multiply b with sin C divided by sin B which gives, c = (b x sin C) / sin B c = (9 x sin 60) / sin 50 c = 10.175